Fuzzy logic is a fantastic way to represent the rules of your game in a more nuanced way. Perhaps more so than other concepts, fuzzy logic is a very math-heavy topic. Most of the information can be represented purely by mathematical functions. For the sake of teaching the important concepts as they apply to Unity, most of the math has been simplified and implemented using Unity’s built-in features.
In this tutorial, we will take a look at the concepts behind fuzzy logic systems and implement in your AI system. Implementing fuzzy logic will make your game characters more believable and depict real-world attributes.
This article is an excerpt from a book written by Ray Barrera, Aung Sithu Kyaw, and Thet Naing Swe titled Unity 2017 Game AI Programming – Third Edition. This book will help you leverage the power of artificial intelligence to program smart entities for your games.
Defining fuzzy logic
The simplest way to define fuzzy logic is by comparison to binary logic. Generally, transition rules as looked at as true or false or 0 or 1 values. Is something visible? Is it at least a certain distance away? Even in instances where multiple values were being evaluated, all of the values had exactly two outcomes; thus, they were binary. In contrast, fuzzy values represent a much richer range of possibilities, where each value is represented as a float rather than an integer. We stop looking at values as 0 or 1, and we start looking at them as 0 to 1.
A common example used to describe fuzzy logic is temperature. Fuzzy logic allows us to make decisions based on non-specific data. I can step outside on a sunny Californian summer’s day and ascertain that it is warm, without knowing the temperature precisely. Conversely, if I were to find myself in Alaska during the winter, I would know that it is cold, again, without knowing the exact temperature. These concepts of cold, cool, warm, and hot are fuzzy ones. There is a good amount of ambiguity as to at what point we go from warm to hot. Fuzzy logic allows us to model these concepts as sets and determine their validity or truth by using a set of rules.
When people make decisions, people have some gray areas. That is to say, it’s not always black and white. The same concept applies to agents that rely on fuzzy logic. Say you hadn’t eaten in a few hours, and you were starting to feel a little hungry. At which point were you hungry enough to go grab a snack? You could look at the time right after a meal as 0, and 1 would be the point where you approached starvation. The following figure illustrates this point:
When making decisions, there are many factors that determine the ultimate choice. This leads into another aspect of fuzzy logic controllers—they can take into account as much data as necessary. Let’s continue to look at our “should I eat?” example. We’ve only considered one value for making that decision, which is the time since the last time you ate. However, there are other factors that can affect this decision, such as how much energy you’re expending and how lazy you are at that particular moment. Or am I the only one to use that as a deciding factor? Either way, you can see how multiple input values can affect the output, which we can think of as the “likeliness to have another meal.”
Fuzzy logic systems can be very flexible due to their generic nature. You provide input, the fuzzy logic provides an output. What that output means to your game is entirely up to you. We’ve primarily looked at how the inputs would affect a decision, which, in reality, is taking the output and using it in a way the computer, our agent, can understand. However, the output can also be used to determine how much of something to do, how fast something happens, or for how long something happens.
For example, imagine your agent is a car in a sci-fi racing game that has a “nitro-boost” ability that lets it expend a resource to go faster. Our 0 to 1 value can represent a normalized amount of time for it to use that boost or perhaps a normalized amount of fuel to use.
Picking fuzzy systems over binary systems
With most things in game programming, we must evaluate the requirements of our game and the technology and hardware limitations when deciding on the best way to tackle a problem.
As you might imagine, there is a performance cost associated with going from a simple yes/no system to a more nuanced fuzzy logic one, which is one of the reasons we may opt out of using it. Of course, being a more complex system doesn’t necessarily always mean it’s a better one. There will be times when you just want the simplicity and predictability of a binary system because it may fit your game better.
While there is some truth to the old adage, “the simpler, the better”, one should also take into account the saying, “everything should be made as simple as possible, but not simpler”. Though the quote is widely attributed to Albert Einstein, the father of relativity, it’s not entirely clear who said it. The important thing to consider is the meaning of the quote itself. You should make your AI as simple as your game needs it to be, but not simpler. Pac-Man’s AI works perfectly for the game–it’s simple enough. However, rules say that simple would be out of place in a modern shooter or strategy game.
Using fuzzy logic
Once you understand the simple concepts behind fuzzy logic, it’s easy to start thinking of the many ways in which it can be useful. In reality, it’s just another tool in our belt, and each job requires different tools.
Fuzzy logic is great at taking some data, evaluating it in a similar way to how a human would (albeit in a much simpler way), and then translating the data back to information that is usable by the system.
Fuzzy logic controllers have several real-world use cases. Some are more obvious than others, and while these are by no means one-to-one comparisons to our usage in game AI, they serve to illustrate a point:
- Heating ventilation and air conditioning (HVAC) systems: The temperature example when talking about fuzzy logic is not only a good theoretical approach to explaining fuzzy logic, but also a very common real-world example of fuzzy logic controllers in action.
- Automobiles: Modern automobiles come equipped with very sophisticated computerized systems, from the air conditioning system (again), to fuel delivery, to automated braking systems. In fact, putting computers in automobiles has resulted in far more efficient systems than the old binary systems that were sometimes used.
- Your smartphone: Ever notice how your screen dims and brightens depending on how much ambient light there is? Modern smartphone operating systems look at ambient light, the color of the data being displayed, and the current battery life to optimize screen brightness.
- Washing machines: Not my washing machine necessarily, as it’s quite old, but most modern washers (from the last 20 years) make some use of fuzzy logic. Load size, water dirtiness, temperature, and other factors are taken into account from cycle to cycle to optimize water use, energy consumption, and time.
If you take a look around your house, there is a good chance you’ll find a few interesting uses of fuzzy logic, and I mean besides your computer, of course. While these are neat uses of the concept, they’re not particularly exciting or game-related. I’m partial to games involving wizards, magic, and monsters, so let’s look at a more relevant example.
Implementing a simple fuzzy logic system
For this example, we’re going to use my good friend, Bob, the wizard. Bob lives in an RPG world, and he has some very powerful healing magic at his disposal. Bob has to decide when to cast this magic on himself based on his remaining health points (HPs).
In a binary system, Bob’s decision-making process might look like this:
if(healthPoints <= 50)
{
CastHealingSpell(me);
}
We see that Bob’s health can be in one of two states—above 50, or not. Nothing wrong with that, but let’s have a look at what the fuzzy version of this same scenario might look like, starting with determining Bob’s health status:
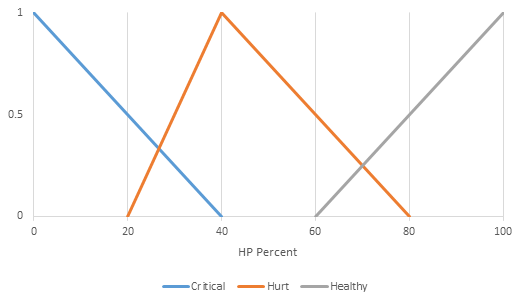
Before the panic sets in upon seeing charts and values that may not quite mean anything to you right away, let’s dissect what we’re looking at. Our first impulse might be to try to map the probability that Bob will cast a healing spell to how much health he is missing. That would, in simple terms, just be a linear function. Nothing really fuzzy about that—it’s a linear relationship, and while it is a step above a binary decision in terms of complexity, it’s still not truly fuzzy.
Enter the concept of a membership function. It’s key to our system, as it allows us to determine how true a statement is. In this example, we’re not simply looking at raw values to determine whether or not Bob should cast his spell; instead, we’re breaking it up into logical chunks of information for Bob to use in order to determine what his course of action should be.
In this example, we’re comparing three statements and evaluating not only how true each one is, but which is the most true:
- Bob is in a critical condition
- Bob is hurt
- Bob is healthy
If you’re into official terminology, we call this determining the degree of membership to a set. Once we have this information, our agent can determine what to do with it next.
At a glance, you’ll notice it’s possible for two statements to be true at a time. Bob can be in a critical condition and hurt. He can also be somewhat hurt and a little bit healthy. You’re free to pick the thresholds for each, but, in this example, let’s evaluate these statements as per the preceding graph. The vertical value represents the degree of truth of a statement as a normalized float (0 to 1):
- At 0 percent health, we can see that the critical statement evaluates to 1. It is absolutely true that Bob is critical when his health is gone.
- At 40 percent health, Bob is hurt, and that is the truest statement.
- At 100 percent health, the truest statement is that Bob is healthy.
Anything outside of these absolutely true statements is squarely in fuzzy territory. For example, let’s say Bob’s health is at 65 percent. In that same chart, we can visualize it like this:
The vertical line drawn through the chart at 65 represents Bob’s health. As we can see, it intersects both sets, which means that Bob is a little bit hurt, but he’s also kind of healthy. At a glance, we can tell, however, that the vertical line intercepts the Hurt set at a higher point in the graph. We can take this to mean that Bob is more hurt than he is healthy. To be specific, Bob is 37.5 percent hurt, 12.5 percent healthy, and 0 percent critical. Let’s take a look at this in code; open up our FuzzySample scene in Unity. The hierarchy will look like this:
The important game object to look at is Fuzzy Example. This contains the logic that we’ll be looking at. In addition to that, we have our Canvas containing all of the labels and the input field and button that make this example work. Lastly, there’s the Unity-generated EventSystem and Main Camera, which we can disregard. There isn’t anything special going on with the setup for the scene, but it’s a good idea to become familiar with it, and you are encouraged to poke around and tweak it to your heart’s content after we’ve looked at why everything is there and what it all does.
With the Fuzzy Example game object selected, the inspector will look similar to the following image:
Our sample implementation is not necessarily something you’ll take and implement in your game as it is, but it is meant to illustrate the previous points in a clear manner. We use Unity’s AnimationCurve for each different set. It’s a quick and easy way to visualize the very same lines in our earlier graph.
Unfortunately, there is no straightforward way to plot all the lines in the same graph, so we use a separate AnimationCurve for each set. In the preceding screenshot, they are labeled Critical, Hurt, and Healthy. The neat thing about these curves is that they come with a built-in method to evaluate them at a given point (t). For us, t does not represent time, but rather the amount of health Bob has.
As in the preceding graph, the Unity example looks at a HP range of 0 to 100. These curves also provide a simple user interface for editing the values. You can simply click on the curve in the inspector. That opens up the curve editing window. You can add points, move points, change tangents, and so on, as shown in the following screenshot:
Unity’s curve editor window
Our example focuses on triangle-shaped sets. That is, linear graphs for each set. You are by no means restricted to this shape, though it is the most common. You could use a bell curve or a trapezoid, for that matter. To keep things simple, we’ll stick to the triangle.
You can learn more about Unity’s AnimationCurve editor at http://docs.unity3d.com/ScriptReference/AnimationCurve.html.
The rest of the fields are just references to the different UI elements used in code that we’ll be looking at later in this chapter. The names of these variables are fairly self-explanatory, however, so there isn’t much guesswork to be done here.
Next, we can take a look at how the scene is set up. If you play the scene, the game view will look something similar to the following screenshot:
A simple UI to demonstrate fuzzy values
We can see that we have three distinct groups, representing each question from the “Bob, the wizard” example. How healthy is Bob, how hurt is Bob, and how critical is Bob? For each set, upon evaluation, the value that starts off as 0 true will dynamically adjust to represent the actual degree of membership.
There is an input box in which you can type a percentage of health to use for the test. No fancy controls are in place for this, so be sure to enter a value from 0 to 100. For the sake of consistency, let’s enter a value of 65 into the box and then press the Evaluate! button.
This will run some code, look at the curves, and yield the exact same results we saw in our graph earlier. While this shouldn’t come as a surprise (the math is what it is, after all), there are fewer things more important in game programming than testing your assumptions, and sure enough, we’ve tested and verified our earlier statement.
After running the test by hitting the Evaluate! button, the game scene will look similar to the following screenshot:
This is how Bob is doing at 65 percent health
Again, the values turn out to be 0.125 (or 12.5 percent) healthy and 0.375 (or 37.5 percent) hurt. At this point, we’re still not doing anything with this data, but let’s take a look at the code that’s handling everything:
using UnityEngine;
using UnityEngine.UI;
using System.Collections;
public class FuzzySample1 : MonoBehaviour {
private const string labelText = "{0} true";
public AnimationCurve critical;
public AnimationCurve hurt;
public AnimationCurve healthy;
public InputField healthInput;
public Text healthyLabel;
public Text hurtLabel;
public Text criticalLabel;
private float criticalValue = 0f;
private float hurtValue = 0f;
private float healthyValue = 0f;
We start off by declaring some variables. The labelText is simply a constant we use to plug into our label. We replace {0} with the real value.
Next, we declare the three AnimationCurve variables that we mentioned earlier. Making these public or otherwise accessible from the inspector is key to being able to edit them visually (though it is possible to construct curves by code), which is the whole point of using them.
The following four variables are just references to UI elements that we saw earlier in the screenshot of our inspector, and the last three variables are the actual float values that our curves will evaluate into:
private void Start () {
SetLabels();
}
/*
* Evaluates all the curves and returns float values
*/
public void EvaluateStatements() {
if (string.IsNullOrEmpty(healthInput.text)) {
return;
}
float inputValue = float.Parse(healthInput.text);
healthyValue = healthy.Evaluate(inputValue);
hurtValue = hurt.Evaluate(inputValue);
criticalValue = critical.Evaluate(inputValue);
SetLabels();
}
The Start() method doesn’t require much explanation. We simply update our labels here so that they initialize to something other than the default text. The EvaluateStatements() method is much more interesting. We first do some simple null checking for our input string. We don’t want to try and parse an empty string, so we return out of the function if it is empty. As mentioned earlier, there is no check in place to validate that you’ve input a numerical value, so be sure not to accidentally input a non-numerical value or you’ll get an error.
For each of the AnimationCurve variables, we call the Evaluate(float t) method, where we replace t with the parsed value we get from the input field. In the example we ran, that value would be 65. Then, we update our labels once again to display the values we got. The code looks similar to this:
/*
* Updates the GUI with the evluated values based
* on the health percentage entered by the
* user.
*/
private void SetLabels() {
healthyLabel.text = string.Format(labelText, healthyValue);
hurtLabel.text = string.Format(labelText, hurtValue);
criticalLabel.text = string.Format(labelText, criticalValue);
}
}
We simply take each label and replace the text with a formatted version of our labelText constant that replaces the {0} with the real value.
To summarize, we learned how fuzzy logic is used in the real world, and how it can help illustrate vague concepts in a way binary systems cannot. We also learned to implement our own fuzzy logic controllers using the concepts of member functions, degrees of membership, and fuzzy sets.
If you enjoyed this excerpt, check out the book Unity 2017 Game AI Programming – Third Edition, to build exciting and richer games by mastering advanced Artificial Intelligence concepts in Unity.
Read Next:
Unity Machine Learning Agents: Transforming Games with Artificial Intelligence
